Hier geht es zur Hauptseite und zum Impressum
Auf dieser Seite finden Sie Programme für Windows.
Die früheren und einfacheren Programme stehen unten, die späteren Programme stehen oben.
Übersicht:
Datenbank
Primzahlzauber
Viehkauf nach Adam Ries
Klauber-Dreieck
Ulam-Spirale
Primfaktorzerlegung
Zeitmessung mit C#
Überblick über das Kirchenjahr
Osterrechnung nach Gauß
Wochentag und Datum
Datumsrechnung
Logistische Gleichung
Vorsicht Falle!
Sitzzuteilung
Wochentag
Quersumme
Römische Zahlen
Primzahltest
Goldbachsche Vermutung
Palindrome
Primzahlpalindrome
Euklidischer Algorithmus
Sphenische Zahlen
Sphenische Zwillingszahlen
Sphenische Drillingszahlen
Teilermenge
Teilersummen
Befreundete Zahlen
Summe von Kubikzahlen
Pythagoreische Tripel
etwas Zinsrechnung
Datenbank
Mit diesem Programm kann man auf eine Datenbank (Access) mit SQL-Befehlen zugreifen.
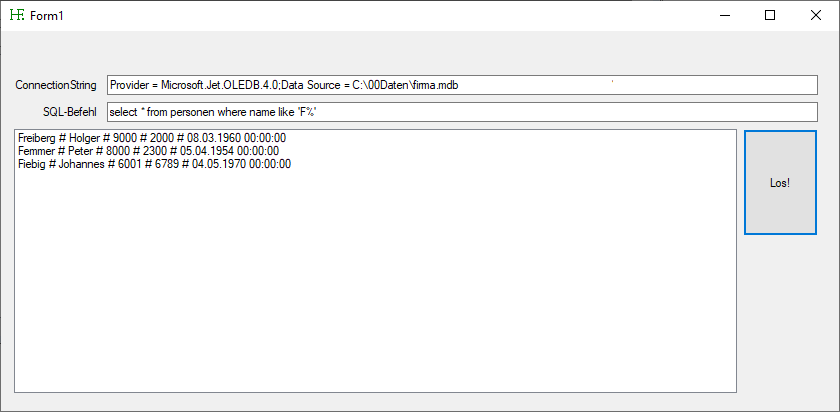
Hier sehen Sie die form1.cs:
using System;
using System.Data.OleDb;
using System.Windows.Forms;
namespace W0049DBMeines
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void Form1_Load(object sender, EventArgs e)
{
textBox1.Text = "Provider = Microsoft.Jet.OLEDB.4.0;" +
"Data Source = C:\\00Daten1\\Users\\kerstin\\Documents\\Datenbanken\\firma.mdb";
}
private void button1_Click(object sender, EventArgs e)
{
OleDbConnection con = new OleDbConnection();
OleDbCommand cmd = new OleDbCommand();
OleDbDataReader reader;
con.ConnectionString = textBox1.Text;
cmd.Connection = con;
cmd.CommandText = textBox2.Text;
try
{
con.Open();
reader = cmd.ExecuteReader();
listBox1.Items.Clear();
while (reader.Read())
{
listBox1.Items.Add(
reader["name"] + " # " +
reader["vorname"] + " # " +
reader["personalnummer"] + " # " +
reader["gehalt"] + " # " +
reader["geburtstag"]);
}
reader.Close();
con.Close();
}
catch(Exception ex)
{
MessageBox.Show(ex.Message);
}
}
}
}
Primzahlzauber
Dieses Programm ist etwas umfangreicher. Mit ihm kann man Primzahlen, Primzahllücken, Primzahlzwillinge, Primzahldrillinge und Primzahlvierlinge berechnen.
Zunächst bildet das Programm ein Sieb des Eratosthenes im Arbeitsspeicher. Das dauert einige Minuten. Erst danach erscheint das Formular.
Ein paar Bemerkungen zu Primzahllücken:
Der Abstand zwischen zwei Primzahlen ist stets gerade (bis auf den Abstand zwischen 2 und 3), da alle Primzahlen ungerade sind (bis auf die 2).
Das Programm errechnet das erstmalige Vorkommen von Primzahllücken für Zahlen bis 2 Milliarden.
Primzahlzwillinge sind jeweils zwei Primzahlen, die sich um 2 unterscheiden.
Primzahldrillinge sind drei aufeinander folgende Primzahlen der Form (n, n+2, n+6) oder (n, n+4, n+6).
Primzahlvierlinge sind vier aufeinander folgende Primzahlen der Form (n, n+2, n+6, n+8).
Hier sehen Sie einen Screenshot des Programms:
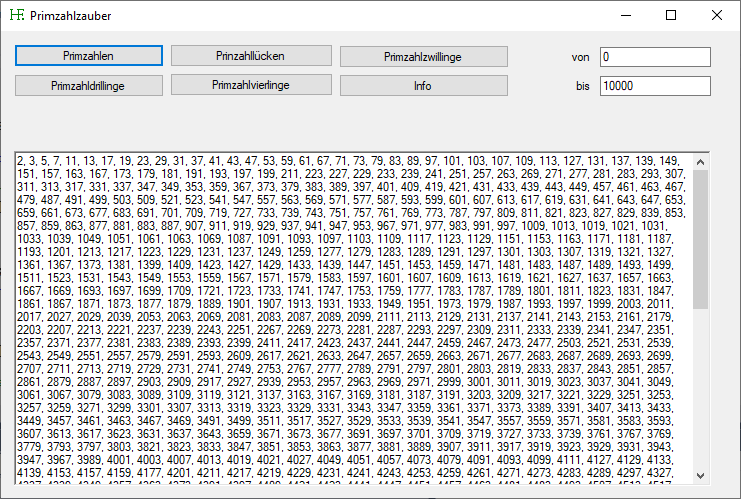
Das Programm herunterladen
Hier sehen Sie die form1.cs:
using System;
using System.Windows.Forms;
namespace Primzahlzauber
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
bool[] nonprime = new bool[2000000000]; // all elements are false (zero)
private void Form1_Load(object sender, EventArgs e)
{
//erzeugt ein Sieb des Eratosthenes
nonprime[0] = nonprime[1] = true;
int pn = 2;
do
{
for (int n = pn * pn; n < 2000000000; n = n + pn)
nonprime[n] = true;
do
{
pn++;
} while (nonprime[pn] == true); //find next prime
} while (pn < 44721);
//Am Ende sind alle Primzahlen "false" und alle Nichtprimzahlen "true"
}
private void button1_Click(object sender, EventArgs e)
{
//Button "Primzahlen"
richTextBox1.Text = "";
int Min=0, Max=0, Zwischen;
try
{
Min = Convert.ToInt32(VontextBox.Text);
Max = Convert.ToInt32(BistextBox.Text);
}
catch (Exception ex)
{
lblAusgabe.Text = "Fehler: " + ex.Message; //Ausgabe des Fehlers in deutsch
}
if (Min >= Max)
{
Zwischen = Min;
Min = Max;
Max = Zwischen;
}
for (int x = Min; x= Max)
{
Zwischen = Min;
Min = Max;
Max = Zwischen;
}
for (int x = Min; x < Max; x++)
{
if (nonprime[x] == false)
if (nonprime[x+2]==false)
richTextBox1.Text += x + " " + (x+2) + ", ";
}
}
private void button4_Click(object sender, EventArgs e)
{
//Button "Primzahldrillinge"
richTextBox1.Text = "";
int Min = 0, Max = 0, Zwischen;
try
{
Min = Convert.ToInt32(VontextBox.Text);
Max = Convert.ToInt32(BistextBox.Text);
}
catch (Exception ex)
{
lblAusgabe.Text = "Fehler: " + ex.Message; //Ausgabe des Fehlers in deutsch
}
if (Min >= Max)
{
Zwischen = Min;
Min = Max;
Max = Zwischen;
}
for (int x = Min; x < Max; x++)
{
if (nonprime[x] == false)
if (nonprime[x + 2] == false)
if (nonprime[x + 6] == false)
richTextBox1.Text += x + " " + (x + 2) + " " + (x + 6) + ", ";
if (nonprime[x] == false)
if (nonprime[x + 4] == false)
if (nonprime[x + 6] == false)
richTextBox1.Text += x + " " + (x + 4) + " " + (x + 6) + ", ";
}
}
private void button5_Click(object sender, EventArgs e)
{
//Button "Primzahlvierlinge"
richTextBox1.Text = "";
int Min = 0, Max = 0, Zwischen;
try
{
Min = Convert.ToInt32(VontextBox.Text);
Max = Convert.ToInt32(BistextBox.Text);
}
catch (Exception ex)
{
lblAusgabe.Text = "Fehler: " + ex.Message; //Ausgabe des Fehlers in deutsch
}
if (Min >= Max)
{
Zwischen = Min;
Min = Max;
Max = Zwischen;
}
for (int x = Min; x < Max; x++)
{
if (nonprime[x] == false)
if (nonprime[x + 2] == false)
if (nonprime[x + 6] == false)
if (nonprime[x + 8] == false)
richTextBox1.Text += x + " " + (x + 2) + " " + (x + 6) + " " + (x + 8)+ ", ";
}
}
private void button6_Click(object sender, EventArgs e)
{
//Button "Info"
MessageBox.Show(
"Mehr kostenlose Programme gibt's auf www.holger-freydank.de!",
"Info",
MessageBoxButtons.OK,
MessageBoxIcon.Information,
MessageBoxDefaultButton.Button1,0,
"https://www.holger-freydank.de");
}
}
}
Viehkauf nach Adam Ries
Der Rechenmeister Adam Ries stellte folgende Aufgabe:
Jemand hat 100 Gulden und will 100 Stück Vieh kaufen, und zwar Ochsen, Schweine, Kälber und Ziegen.
1 Ochse kostet 4 Gulden.
1 Schwein kostet 1.5 Gulden.
1 Kalb kostet 0.5 Gulden.
1 Ziege kostet 0.25 Gulden.
Wieviel Tiere von jeder Art soll er kaufen?
Die Aufgabe hat keine eindeutige Lösung, da wir es mit 4 Unbekannten und nur zwei Gleichungen zu tun haben.
1. Gleichung: (Anzahl der Tiere) w + x + y + z = 100
2. Gleichung: (Geld) 4*w + 1.5*x + 0.5*y + 0.25*z = 100
Das Programm ermittelt alle möglichen Lösungen (es sind genau 222).
Dazu arbeitet es mit 4 ineinander geschachtelten for-Schleifen (für jede der 4 Vieharten je eine), die alle möglichen
Kombinationen ermitteln. In der innersten for-Schleife werden die gesuchten Varianten "herausgefischt"
(100 Gulden Gesamtpreis, 100 Tiere insgesamt) und ausgegeben.
Hier sehen Sie einen Screenshot des Programms:
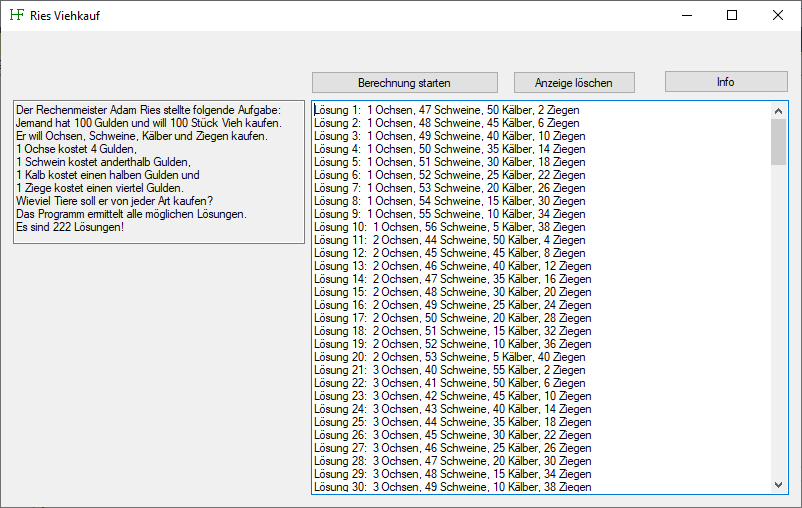
Das Programm herunterladen
Hier sehen Sie die form1.cs:
using System;
using System.Windows.Forms;
namespace Viehkauf
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void Button1_Click(object sender, EventArgs e)
{
int[] tiere = new int[4];
tiere[0] = tiere[1] = tiere[2] = tiere[3] = 1;
int Zahl, Loesung = 0;
double Geld = 0;
for(int l=1; l<= 97; l++)
{
tiere[3] = l;
for (int k = 1; k <= 97; k++)
{
tiere[2] = k;
for(int j=1; j<=97; j++)
{
tiere[1] = j;
for(int i=1; i<=97; i++)
{
tiere[0] = i;
Geld = tiere[0] * 0.25 + tiere[1] * 0.5 + tiere[2] * 1.5 + tiere[3] * 4.0;
Zahl = tiere[0] + tiere[1] + tiere[2] + tiere[3];
if (Geld == 100 && Zahl == 100)
{
Loesung++;
textBox1.Text += "Lösung " + Loesung + ": " + tiere[3] + " Ochsen, " + tiere[2] + " Schweine, " +
tiere[1] + " Kälber, " + tiere[0] + " Ziegen" + "\r\n";
}
}
}
}
}
}
private void Button2_Click(object sender, EventArgs e)
{
//Textbox löschen
textBox1.Text = "";
}
private void CmdInfo_Click(object sender, EventArgs e)
{
MessageBox.Show(
"Mehr kostenlose Programme gibt's auf www.holger-freydank.de!",
"Info",
MessageBoxButtons.OK,
MessageBoxIcon.Information,
MessageBoxDefaultButton.Button1,
0,
"https://www.holger-freydank.de"
);
}
}
}
Klauber-Dreieck
Klauber war ein amerikanischer Mathematiker. Er ordnete Zahlen in Form eines Dreiecks an:

Dabei sind die Primzahlen rot umrandet.
Das Programm zeichnet ein Klauber-Dreieck. Die Primzahlen erscheinen als schwarze Pixel.
Hier sehen Sie einen Screenshot des Programms:
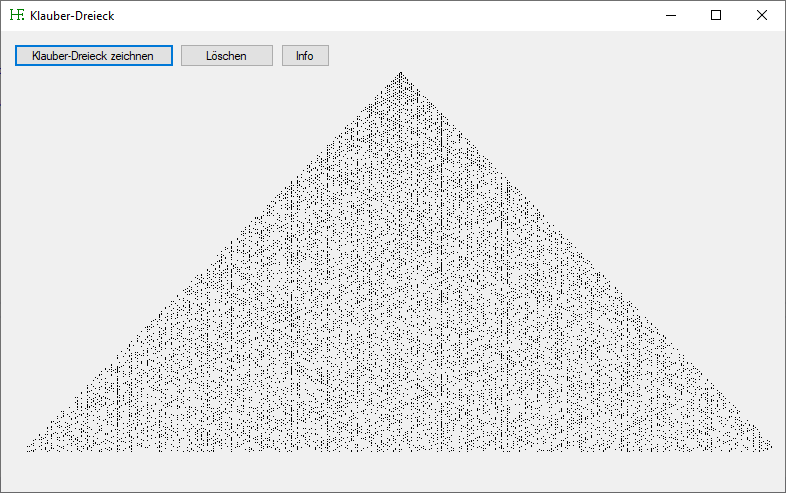
Das Programm herunterladen
Hier sehen sie die form1.cs:
using System;
using System.Drawing;
using System.Windows.Forms;
namespace KlauberDreieck
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
Graphics z;
private void CmdStart_Click(object sender, EventArgs e)
{
//erstellt ein Sieb des Eratosthenes für alle Zahlen unter 150000
bool[] nonprime = new bool[150000]; // all elements are false (zero)
nonprime[0] = nonprime[1] = true;
int pn = 2;
do
{
for (int n = pn * pn; n < 150000; n = n + pn)
nonprime[n] = true; //Streichen der Zahlen
do
{
pn++;
} while (nonprime[pn] == true); //find next prime
} while (pn < 387);
//Am Ende sind alle Primzahlen "false" und alle Nichtprimzahlen "true"
int x, y, zahl, zeile, startx, starty;
zahl = 2; zeile = 1; //zeile: Anzahl der Zahlen in einer Zeile
startx = 400;
starty = 40;
for (int k=0; k<380; k++)
{
starty++;
startx--;
zeile = zeile + 2;
x = startx;
y = starty;
for(int i = 0; i < zeile; i++)
{
if (nonprime[zahl] == false)
z.FillRectangle(Brushes.Black, x, y, 1, 1);
zahl++;
x++;
}
}
}
private void Form1_Load(object sender, EventArgs e)
{
z = CreateGraphics();
}
private void CmdClear_Click(object sender, EventArgs e)
{
z.Clear(BackColor);
}
}
}
Ulam-Spirale
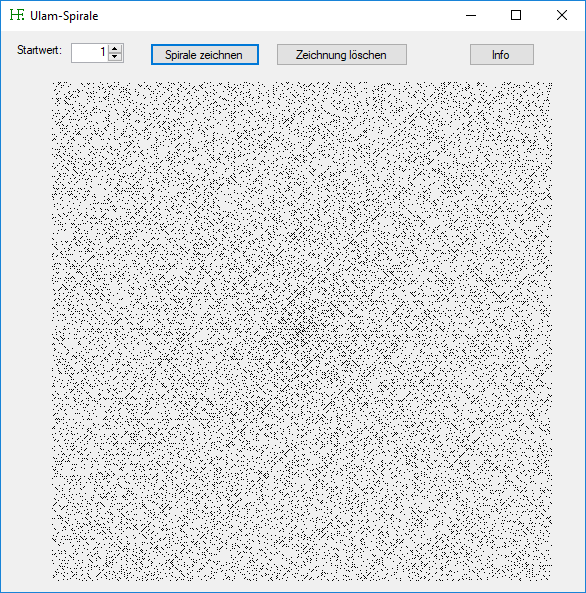
Stanislaw Ulam war ein polnischer Mathematiker, der unter anderem am amerikanschen Atombomben-Programm beteiligt war. Eines Tages im Jahre 1963 hörte er einen etwas langweiligen wissenschaftlichen Vortrag. Er begann, Zahlen in einer Spirale aufzuschreiben und dann die Primzahlen einzukreisen. Dabei erhielt er folgendes Muster:

Auffällig sind die Diagonalen, auf denen sich Primzahlen befinden.
Das Programm zeichnet eine Ulam-Spirale mit einer Seitenlänge von 500 Pixeln. Es kann ein Startwert eingegeben werden. Primzahlen erscheinen als schwarze Pixel.
Hier sehen Sie einen Screenshot des Programms:
Das Programm herunterladen
Hier sehen sie die form1.cs:
using System;
using System.Drawing;
using System.Windows.Forms;
namespace UlamSpirale
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
Graphics z;
private void CmdStart_Click(object sender, EventArgs e)
{
//erstellt ein Sieb des Eratosthenes für alle Zahlen unter 400000
bool[] nonprime = new bool[400000]; // all elements are false (zero)
nonprime[0] = nonprime[1] = true;
int pn = 2;
do
{
for (int n = pn*pn ; n < 400000; n = n + pn)
nonprime[n] = true;
do
{
pn++;
} while (nonprime[pn] == true); //find next prime
} while (pn <= 632);
//Am Ende sind alle Primzahlen "false" und alle Nichtprimzahlen "true"
int zahl, x, y; // die Koordinaten
x = y = 300; // Startwert der Koordinaten
zahl = (int)numericUpDown1.Value; // Startwert
byte modus = 1;
for (int zaehler = 1; zaehler < 500; zaehler++)
{
for(int i=0; i < zaehler;i++)
{
if(nonprime[zahl] == false)
z.FillRectangle(Brushes.Black, x, y, 1, 1);
zahl++;
if (modus == 1) x++; //nach rechts
if (modus == 2) y--; //nach oben
if (modus == 3) x--; //nach links
if (modus == 4) y++; //nach unten
}
modus++;
if (modus == 5) modus = 1;
for (int i = 0; i < zaehler; i++)
{
if (nonprime[zahl] == false)
z.FillRectangle(Brushes.Black, x, y, 1, 1);
zahl++;
if (modus == 1) x++;
if (modus == 2) y--;
if (modus == 3) x--;
if (modus == 4) y++;
}
modus++;
if (modus == 5) modus = 1;
}
}
private void Form1_Load(object sender, EventArgs e)
{
z = CreateGraphics();
}
private void CmdClear_Click(object sender, EventArgs e)
{
z.Clear(BackColor);
}
}
}
Primfaktorzerlegung
Zu jeder ganzen Zahl gibt es eine eindeutige Zerlegung in Primfaktoren.
Zum Beispiel lautet die Primfaktorzerlegung von 20: 2*2*5.
Das Programm errechnet die Primfaktorzerlegung oder Primzahlzerlegung einer Zahl mithilfe der Probedivision.
Die Probedivision funktioniert folgendermaßen: Als erstes wird versucht, die Zahl durch die kleinste Primzahl - die zwei - zu dividieren. Ist das möglich, ist der erste Primfaktor gefunden. Nun wird versucht, das Ergebnis wieder durch zwei zu teilen. Ist eine Division durch zwei nicht möglich, wird versucht, durch die nächstgrößere Primzahl zu dividieren, also die drei. Ist das möglich, ist wieder ein Primfaktor gefunden. Nun wird so lange durch drei dividiert, bis keine ganzzahlige Division durch drei möglich ist. Dann wird zur nächstgrößeren Primzahl übergegangen, der fünf. Das ganze wird wiederholt, bis das Ergebnis der jeweiligen Division eins ist. Auf diese Weise erhält man der Reihe nach die Primfaktoren der Zahl.
Noch klarer wird der Algorithmus der Probedivision durch ein Struktogramm:
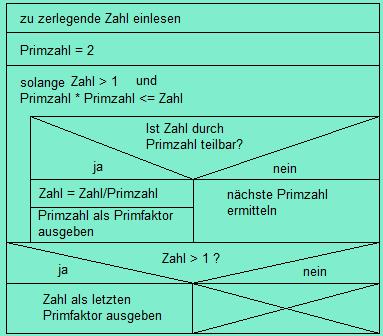
Diese Primfaktorzerlegung wurde mit BigInteger programmiert, mit der man (fast) beliebig große ganze Zahlen verarbeiten kann. Dazu muss man den Namensraum System.Numerics einbinden.
Hier sehen Sie einen Screenshot des Programms:
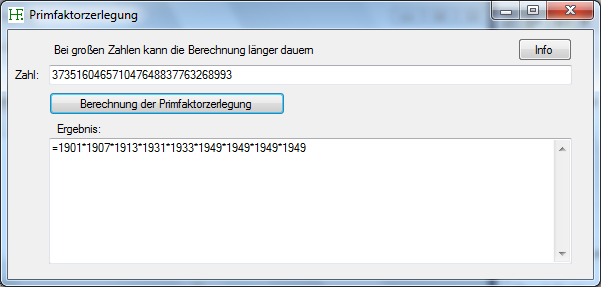
Das Programm herunterladen
Hier sehen sie die form1.cs:
using System;
using System.Numerics;
using System.Windows.Forms;
namespace PFZ
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private BigInteger naechste_primzahl(BigInteger zahl)
{
BigInteger i;
bool primzahl = true;
do
{
if (zahl <= 2) zahl++;
else zahl += 2;
primzahl = true;
BigInteger wurzel = (BigInteger)Math.Exp(BigInteger.Log(zahl) / 2);
for (i = 2; i <= wurzel; i++)
if (zahl % i == 0)
{
primzahl = false;
break;
}
} while (primzahl == false);
return zahl;
}
private void cmdBerechnung_Click(object sender, EventArgs e)
{
BigInteger zahl, primzahl;
textBox2.Text = "";
try
{
zahl = BigInteger.Parse(textBox1.Text);
primzahl = 2;
if (zahl > 1)
textBox2.Text += "=";
while (zahl > 1 && primzahl * primzahl <= zahl)
if (zahl % primzahl == 0)
{
textBox2.Text += primzahl.ToString();
zahl /= primzahl;
if (zahl > 1)
textBox2.Text += "*";
}
else
primzahl = naechste_primzahl(primzahl);
if (zahl > 1)
textBox2.Text += zahl.ToString();
}
catch (FormatException)
{
textBox2.Text = "Falsches Eingabeformat";
}
catch (Exception ex)
{
textBox2.Text = "Fehler: " + ex.Message;
}
}
}
}
Zeitmessung mit C#
Manchmal möchte man wissen, wieviel Zeit ein Programm braucht. C# stellt dazu die Klasse Stopwatch bereit. Dazu ist es erforderlich, den Namensraum System.Diagnostics einzubinden.
Es folgt ein Beispiel zur Verwendung von Stopwatch in einer Konsolenanwendung:
using System.Diagnostics;
namespace Zeitmessung
{
class Program
{
static void Main()
{
Stopwatch sw = new Stopwatch();
sw.Start();
//hier läuft das Programm!!
sw.Stop();
TimeSpan ts = sw.Elapsed;
string elapsedTime = String.Format("{0:00}:{1:00}:{2:00}.{3:00}",
ts.Hours, ts.Minutes, ts.Seconds, ts.Milliseconds / 10);
Console.WriteLine("vergangene Zeit: " + elapsedTime);
}
}
}
Kirchenjahr
Dieses Programm liefert eine Übersicht über das Kirchenjahr, z. B. wieviel Sonntage nach Epiphanias und wieviel Sonntage nach Trinitatis es in dem entsprechenden Jahr gibt.
Hier sehen Sie einen Screenshot des Programms:
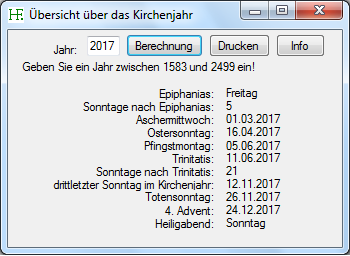
Das Programm herunterladen
Hier sehen sie die form1.cs:
using System;
using System.Windows.Forms;
using System.Globalization;
using Print1 = Microsoft.VisualBasic.PowerPacks.Printing;
using Print2 = System.Drawing.Printing;
namespace Kirchenjahr
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void cmdBerechnung_Click(object sender, EventArgs e)
{
int Jahr;
try
{
Jahr = Convert.ToInt32(txtJahr.Text);
if (Jahr < 1583 || Jahr > 2499)
goto Ende;
int a, b, c, d, E, M = 0, N = 0, Ostern, Monat = 3;
a = Jahr % 19; b = Jahr % 4; c = Jahr % 7;
if (Jahr > 1582 && Jahr < 1700)
{
M = 22; N = 2;
}
if (Jahr >= 1700 && Jahr < 1800)
{
M = 23; N = 3;
}
if (Jahr >= 1800 && Jahr < 1900)
{
M = 23; N = 4;
}
if (Jahr >= 1900 && Jahr < 2000)
{
M = 24; N = 5;
}
if (Jahr >= 2000 && Jahr < 2100)
{
M = 24; N = 5;
}
if (Jahr >= 2100 && Jahr < 2200)
{
M = 24; N = 6;
}
if (Jahr >= 2200 && Jahr < 2300)
{
M = 25; N = 0;
}
if (Jahr >= 2300 && Jahr < 2400)
{
M = 26; N = 1;
}
if (Jahr >= 2400 && Jahr < 2500)
{
M = 25; N = 1;
}
d = (19 * a + M) % 30; E = (2 * b + 4 * c + 6 * d + N) % 7;
Ostern = d + E + 22;
if (Ostern > 31)
{
Ostern = Ostern - 31;
Monat = 4;
}
if (Ostern == 26 && Monat == 4)
Ostern = 19;
if (Ostern == 25 && Monat == 4 && a == 10 && d == 28)
Ostern = 18;
var culture = new CultureInfo("de-DE");
DateTime weihnacht = new DateTime(Jahr, 12, 24); //24.12.
var day = culture.DateTimeFormat.GetDayName(weihnacht.DayOfWeek);
lblErgHeiligabend.Text = "" + day;
TimeSpan ts1 = new TimeSpan((int)weihnacht.DayOfWeek, 0, 0, 0);
DateTime advent4 = new DateTime();
advent4 = weihnacht.Subtract(ts1);
lblErg4Advent.Text = "" + advent4.ToShortDateString(); //4. Advent
TimeSpan wochen4 = new TimeSpan(28, 0, 0, 0);
DateTime totensonntag = advent4.Subtract(wochen4);
lblErgTotensonntag.Text = totensonntag.ToShortDateString();
DateTime ostern = new DateTime(Jahr, Monat, Ostern);
lblErgOstersonntag.Text = "" + ostern.ToShortDateString();
DateTime pfingsten = ostern.AddDays(50);
lblErgPfingstmontag.Text = "" + pfingsten.ToShortDateString();
DateTime trinitatis = ostern.AddDays(56);
lblErgTrinitatis.Text = "" + trinitatis.ToShortDateString();
DateTime drittletztersonntagnachtrinitatis = totensonntag.AddDays(-14);
lblErgdrittletzter_Sonntag_nach_Trinitatis.Text = "" +
drittletztersonntagnachtrinitatis.ToShortDateString();
int sonntagenachtrinitatis = (drittletztersonntagnachtrinitatis.DayOfYear -
trinitatis.DayOfYear) / 7 - 1;
lblErgSonntageNachTrinitatis.Text = "" + sonntagenachtrinitatis;
DateTime aschermittwoch = ostern.AddDays(-46);
lblErgAschermittwoch.Text = "" + aschermittwoch.ToShortDateString();
DateTime epiphanias = new DateTime(Jahr, 1, 6);
var day2 = culture.DateTimeFormat.GetDayName(epiphanias.DayOfWeek);
lblErgEpiphanias.Text = "" + day2;
DateTime septuagesimae = ostern.AddDays(-63);
int differenz;
if (epiphanias.DayOfWeek == 0)
differenz = (septuagesimae.DayOfYear - epiphanias.DayOfYear) / 7 - 1;
else
differenz = (septuagesimae.DayOfYear - epiphanias.DayOfYear) / 7;
lblErgSonntage_nach_Epiphanias.Text = "" + differenz;
Ende:
lblAusgabe.Text = "Geben Sie ein Jahr zwischen 1583 und 2499 ein!";
}
catch(Exception)
{
lblAusgabe.Text= "Geben Sie ein Jahr zwischen 1583 und 2499 ein!";
}
}
private void cmdInfo_Click(object sender, EventArgs e)
{
MessageBox.Show(
"Mehr kostenlose Programme gibt's auf www.holger-freydank.de!",
"Info",
MessageBoxButtons.OK,
MessageBoxIcon.Information,
MessageBoxDefaultButton.Button1,
0,
"http://www.holger-freydank.de"
);
}
//Der Button heißt eigentlich cmdDrucken
//aus Versehen habe ich auf den ursprünglichen Button
//doppelgeklickt und dadurch diese Ereignismethode erzeugt
private void button1_Click(object sender, EventArgs e)
{
Print1.PrintForm pf = new Print1.PrintForm();
pf.Form = this;
pf.PrintAction = Print2.PrintAction.PrintToPrinter;
pf.Print();
}
}
}
Ostern
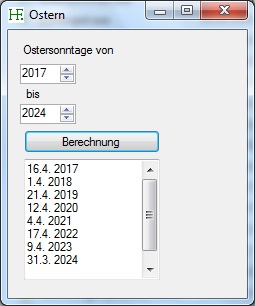
Das folgende Programm in C# ermittelt die Ostersonntage zwischen zwei Grenzen. Berechnet wird nach der von Gauß entwickelten Formel. Gültig ist das Verfahren zwischen den Jahren 1583 und 2500.
Das Ergebnis wird in eine TextBox ausgegeben und kann dann nach Markieren in die Zwischenablage kopiert werden.
Hier sehen Sie einen Screenshot des Programmes:
Das Programm herunterladen
Hier sehen sie die form1.cs:
using System;
using System.Windows.Forms;
namespace Ostern
{
public partial class Ostern : Form
{
public Ostern()
{
InitializeComponent();
}
private void cmdBerechnung_Click(object sender, EventArgs e)
{
textBox1.Text = "";
if (numericUpDown1.Value > numericUpDown2.Value)
{
MessageBox.Show(
"Wert 1 ist größer als Wert 2!", "Fehler",
MessageBoxButtons.OK);
}
for (int Jahr = (int)numericUpDown1.Value; Jahr <= (int)numericUpDown2.Value; Jahr++)
{
int a, b, c, d, E, M=0, N=0, Ostern, Monat=3;
a = Jahr % 19; b = Jahr % 4; c = Jahr % 7;
if (Jahr > 1582 && Jahr < 1700)
{
M = 22; N = 2;
}
if (Jahr >= 1700 && Jahr < 1800)
{
M = 23; N = 3;
}
if (Jahr >= 1800 && Jahr < 1900)
{
M = 23; N = 4;
}
if (Jahr >= 1900 && Jahr < 2000)
{
M = 24; N = 5;
}
if (Jahr >= 2000 && Jahr < 2100)
{
M = 24; N = 5;
}
if (Jahr >= 2100 && Jahr < 2200)
{
M = 24; N = 6;
}
if (Jahr >= 2200 && Jahr < 2300)
{
M = 25; N = 0;
}
if (Jahr >= 2300 && Jahr < 2400)
{
M = 26; N = 1;
}
if (Jahr >= 2400 && Jahr < 2500)
{
M = 25; N = 1;
}
d = (19 * a + M) % 30; E = (2 * b + 4 * c + 6 * d + N) % 7;
Ostern = d + E + 22;
if(Ostern > 31)
{
Ostern = Ostern - 31;
Monat = 4;
}
if (Ostern == 26 && Monat == 4)
Ostern = 19;
if (Ostern == 25 && Monat == 4 && a == 10 && d == 28)
Ostern = 18;
textBox1.Text += Ostern + "." + Monat + "." + " "+ Jahr + "\r\n";
}
}
private void numericUpDown1_ValueChanged(object sender, EventArgs e)
{
}
}
}
Wochentag und Datum
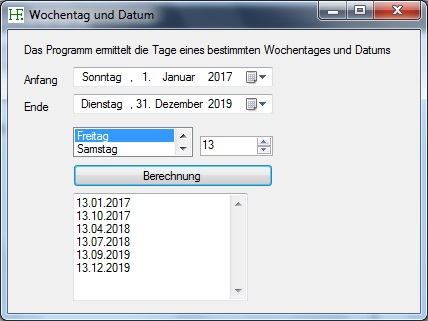
Das folgende Programm ermittelt das Vorkommen eines bestimmten Datums und eines bestimmten Wochentages. Zum Beispiel ermittelt es alle Vorkommen von Freitag, dem 13. zwischen zwei Grenzen.
Das Ergebnis wird in eine TextBox ausgegeben und kann dann nach Markieren in die Zwischenablage kopiert werden.
Hier sehen Sie einen Screenshot des Programmes:
Das Programm herunterladen
Hier sehen sie die form1.cs:
using System;
using System.Windows.Forms;
namespace wochentagdatum
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
decimal Monatstag;
int Wochentag;
private void cmdBerechnung_Click(object sender, EventArgs e)
{
if (datPicker1.Value > datPicker2.Value)
MessageBox.Show(
"Datum1 ist größer als Datum2 !!", "Fehler",
MessageBoxButtons.OK);
textBox1.Text = ""; //textBox1 leeren
DateTime datum = new DateTime();
datum = datPicker1.Value;
Monatstag = numericUpDown1.Value;
Wochentag = listBox1.SelectedIndex;
while (datum < datPicker2.Value)
{
datum = datum.AddDays(1);
if (datum.Day == Monatstag && (int)datum.DayOfWeek == Wochentag)
textBox1.Text += datum.ToShortDateString() + "\r\n";
}
}
private void Form1_Load(object sender, EventArgs e)
{
listBox1.Items.Add("Sonntag");
listBox1.Items.Add("Montag");
listBox1.Items.Add("Dienstag");
listBox1.Items.Add("Mittwoch");
listBox1.Items.Add("Donnerstag");
listBox1.Items.Add("Freitag");
listBox1.Items.Add("Samstag");
}
}
}
Datumsrechnung
C# bietet komfortable Klassen und Steuerelemente zur Rechnung mit Datumsangaben.
Das Steuerelement DateTimePicker ist ein sehr mächtiges Instrument zur Feststellung von Datumsangaben.
Mithilfe der Strukturen DateTime und TimeSpan lässt sich komfortabel mit Datumsangaben rechnen.
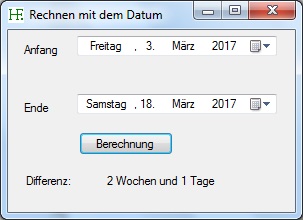
Ich habe ein Programm geschrieben, das die Differenz zweier Datumsangaben in Wochen und Tagen ermittelt.
Die beiden Datumsangaben werden mit DateTimePicker festgestellt.
Hier sehen Sie einen Screenshot des Programmes:
Das Programm herunterladen
Hier sehen sie die form1.cs:
using System;
using System.Drawing;
using System.Windows.Forms;
namespace Datumsrechnung
{
public partial class Form1 : Form
{
TimeSpan differenz = new TimeSpan();
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
differenz = dateTimePicker2.Value - dateTimePicker1.Value;
int wochen = differenz.Days / 7;
int tage = differenz.Days % 7;
lblResult.Text = wochen + " Wochen und " + tage + " Tage";
}
}
}
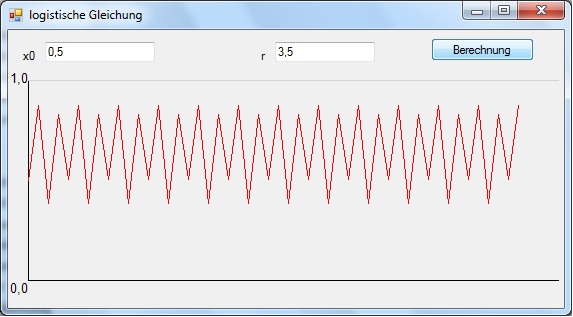
Logistische Gleichung
Dieses Programm zeigt die Berechnung der Logistischen Gleichung.
Hier sehen Sie einen Screenshot des Programmes:
Das Programm herunterladen
Hier sehen sie die form1.cs:
using System;
using System.Drawing;
using System.Windows.Forms;
namespace LogistischeGleichung
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void cmdBerechnung_Click(object sender, EventArgs e)
{
Graphics z = CreateGraphics();
z.Clear(BackColor); //Löschen der vorherigen Zeichng.
Pen stift;
Point start, ende;
Font f = new Font("Arial", 10);
SolidBrush pinsel = new SolidBrush(Color.Black);
try
{
stift = new Pen(Color.Black, 1);
double x0 = Convert.ToDouble(txtx0.Text);
double r = Convert.ToDouble(txtr.Text);
//x-Achse:
z.DrawLine(stift, new Point(20, 250), new Point(550, 250));
//y-Achse:
z.DrawLine(stift, new Point(20, 250), new Point(20, 50));
//1,0 Marke:
z.DrawString("1,0", f, pinsel, 0, 40);
//0,0 Marke:
z.DrawString("0,0", f, pinsel, 0, 250);
stift = new Pen(Color.LightGray);
z.DrawLine(stift, new Point(20, 50), new Point(550, 50));
stift = new Pen(Color.Red, 1);
start = new Point(20, (int)(250 - x0 * 200));
for (int i = 1; i < 50; i++)
{
x0 = r * (x0 - x0 * x0);
ende = new Point(20 + 10 * i, (int)(250 - x0 * 200));
z.DrawLine(stift, start, ende);
start = ende;
}
}
catch (Exception ex)
{
MessageBox.Show("Fehler: " + ex.Message, "Fehler",
MessageBoxButtons.OK);
}
}
}
}
Vorsicht Falle!
Beim Füllen von Feldern können manchmal erstaunliche Effekte auftreten.
Ich wollte ein int-Feld mit Werten füllen.
Die Formel lautete tn[i] = i * (i+1)/2. Ein int-Wert kann maximal 2,14 Mrd. groß sein. Man kann errechnen, dass dann das int-Feld maximal etwa 64000 Werte aufnehmen kann. Soweit so gut.
Im folgenden C#-Programmschnipsel ist es nochmal zu sehen:
using System;
namespace Test
{
class Program
{
static void Main()
{
int[] tn = new int[64000];
for (int i = 0; i < 64000; i++)
tn[i] = i * (i + 1) / 2;
}
}
}
Es begann damit, dass das Programm, in dem das Feld verwendet wurde, seinen Dienst versagte.
Des Rätsels Lösung: Beim Füllen des Feldes errechnet C# ein Zwischenergebnis (i*(i+1)), das größer als der maximale positive Wert für das Feld ist. Das ist aber ein negativer Wert. Dann wird durch zwei dividiert. Heraus kommen in einem großen Teil des Feldes negative Werte, die gar nicht beabsichtigt waren.
Programm "Sitzzuteilung"
Das Programm berechnet die Sitzverteilung nach einer Wahl nach drei Verfahren: d'Hondt, Hare/Niemeyer und Sainte-Lague.
Das Programm ist in C# geschrieben und erfordert das .NET Framework.
Hier sehen sie einen Screenshot des Programms:
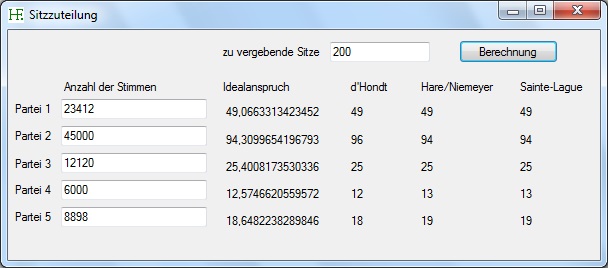
Das Programm herunterladen Die Form1.cs
Programm "Wochentag"
Das Programm ermittelt den Wochentag eines beliebigen Datums vom Jahre 1 bis zum Jahr 9999. Es arbeitet mit der Klasse DateTime von .NET.
Es wird über die Kommandozeile von Windows mit einem Datum aufgerufen. Beispiel:
wt 3.4.2015
Das Programm erfordert das .NET Framework.
Sollte die Fehlermeldung "Side-by-Side-Konfiguration ungültig" erscheinen, müssen Sie sich die Visual C++ Redistributable von Microsoft herunterladen: Link
Das Programm herunterladen C++-Quelle
Programm "Quersumme"
Die Quersumme einer Zahl ist die Summierung der Ziffernwerte dieser Zahl.
Nehmen wir zum Beispiel die Zahl 123. Die Quersumme dieser Zahl beträgt 3+2+1=6.
Um die alternierende Quersumme einer Zahl zu bestimmen, muss man die Ziffernwerte von rechts beginnend abwechselnd addieren und subtrahieren. Dabei
ist die niederwertigste Ziffer zu addieren, die darauf folgende höherwertige zu subtrahieren, die darauf folgende Ziffer wieder zu addieren und so weiter.
Dazu wieder ein Beispiel: Die alternierende Quersumme von 321 ist 1-2+3=2.
Die Quersumme und die alternierende Quersumme spielen eine wichtige Rolle bei der Untersuchung der Teilbarkeit von Zahlen.
Eine Zahl ist dann durch 3 und durch 9 teilbar, wenn ihre Quersumme durch 3 bzw. durch 9 teilbar ist.
Beispiel: 78 ist durch 3 teilbar, weil ihre Quersumme 8+7=15 durch 3 teilbar ist.
81 ist durch 9 teilbar, weil ihre Quersumme 1+8=9 durch 9 teilbar ist.
Schließlich verwendet man die alternierende Quersumme, um die Teilbarkeit durch 11 zu untersuchen. Eine natürliche Zahl ist dann durch 11 teilbar, wenn ihre alternierende Quersumme durch 11 teilbar ist.
Beispiel: 968 ist durch 11 teilbar, weil ihre alternierende Quersumme 8-6+9=11 durch 11 teilbar ist. Auch eine alternierende Quersumme von Null ist durch 11 teilbar, Beispiel: 121.
Das Programm berechnet die Quersumme und die alternierende Quersumme einer Zahl.
Hier ist ein Screenshot des Programms zu sehen:
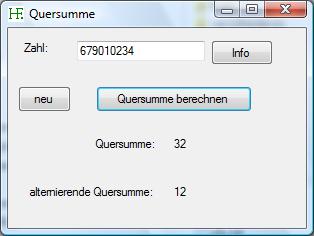
Das Programm herunterladen Ausschnitt aus der form1.h
Programm "Römische Zahlen"
Es rechnet arabische Zahlen in römische Zahlen um.
Das Programm herunterladen C++-Quelle
Programm "Primzahltest"
Es ermittelt zu einer eingegebenen Zahl, ob sie eine Primzahl ist. Windows-Programm!
Das Programm herunterladen
Programm "Goldbachsche Vermutung"
Christian Goldbach war ein Mathematiker im 18. Jahrhundert. Er äußerte die Vermutung, dass sich jede gerade Zahl größer 5 als Summe von zwei ungeraden Primzahlen schreiben lässt. Bis heute ist das weder bewiesen noch widerlegt und gehört zu den ungelösten Problemen der Mathematik.
Bis heute ist noch keine gerade Zahl gefunden worden, die sich NICHT als Summe von zwei ungeraden Primzahlen schreiben lässt.
Im Gegenteil, je größer die Zahl ist, um so mehr Möglichkeiten ihrer Darstellung als Summe von zwei ungeraden Primzahlen gibt es in der Tendenz. Deshalb nehmen heute viele Mathematiker an, dass die Goldbachsche Vermutung wahr ist.
Beispiele:
6 = 3+3
10 = 3+7 = 5+5
26 = 3+23 = 7+19 = 13+13
28 = 5+23 = 11+17
30 = 7+23 = 11+19 = 13+17
48 = 5+43 = 7+41 = 11+37 = 17+31 = 19+29
Das Programm errechnet alle "Goldbachschen Primzahlpaare" zu einer Zahl.
Hier ist ein Screenshot des Programms zu sehen:
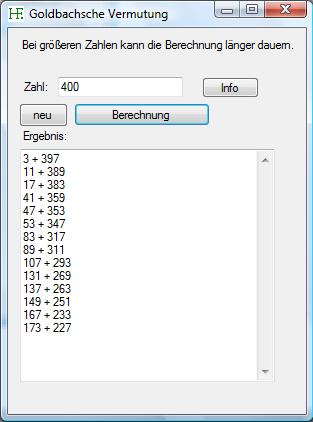
Das Programm herunterladen Ausschnitt aus der form1.h
Programm "Palindrome"
Palindrome oder Palindromzahlen oder symmetrische Zahlen sind Zahlen, die von links und rechts gelesen gleichlauten.
Ein Beispiel ist die Zahl 2552.
Die Palindrome werden auf den Bildschirm und in eine Datei geschrieben.
Das Programm herunterladen C++-Quelle
Programm "Primzahlpalindrome"
Palindromische Primzahlen oder Primzahlpalindrome sind Primzahlen, die von links und von rechts gelesen gleichlauten.
Ein Beispiel ist die Zahl 11 oder die Zahl 131.
Die Primzahlpalindrome werden auf den Bildschirm und in eine Datei geschrieben.
Das Programm herunterladen C++-Quelle
Programm "Euklidischer Algorithmus"
Der euklidische Algorithmus dient zur Berechnung des größten gemeinsamen Teilers zweier natürlicher Zahlen.
Hier ist ein Screenshot des Programms zu sehen:
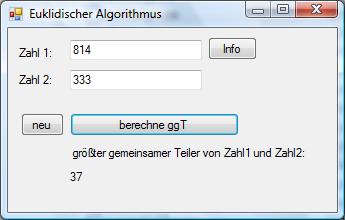
Das Programm herunterladen Ausschnitt aus der form1.h
Programm "Sphenische Zahlen"
Sphenische Zahlen sind Zahlen, die aus genau drei Primzahlen zusammengesetzt sind. Diese Primzahlen sind darüber hinaus paarweise verschieden. Die kleinste sphenische Zahl ist 30 = 2 * 3 * 5. Weitere Beispiele sind 42 = 2 * 3 * 7 und 66 = 2 * 3 * 11.
Die sphenischen Zahlen werden auf den Bildschirm und in eine Datei geschrieben.
Das Programm herunterladen C++-Quelle
Programm "Sphenische Zwillingszahlen"
Sphenische Zwillingszahlen sind sphenische Zahlen, die sich um genau eins unterscheiden.
Die sphenischen Zwillingszahlen werden auf den Bildschirm und in eine Datei geschrieben.
Das Programm herunterladen C++-Quelle
Programm "Sphenische Drillingszahlen"
Sphenische Drillingszahlen sind jeweils drei sphenische Zahlen, die sich um genau eins unterscheiden. Die kleinsten sphenischen Drillingszahlen sind 1309, 1310 und 1311.
Die sphenischen Drillingszahlen werden auf den Bildschirm und in eine Datei geschrieben.
Das Programm herunterladen C++-Quelle
Programm "Teilermenge"
Das Programm errechnet die Teilermenge einer Zahl.
Das Programm herunterladen C++-Quelle
Programm "Teilersummen"
Das Programm errechnet die Teilersummen von Zahlen zwischen zwei Grenzen.
Die Teilersummen werden auf den Bildschirm und in eine Datei geschrieben.
Das Programm herunterladen C++-Quelle
Programm "Befreundete Zahlen"
Befreundete Zahlen sind Paare von Zahlen, die wechselseitig die Summe ihrer echten Teiler sind.
Das kleinste Paar befreundeter Zahlen ist 220 und 284. Das heißt, 284 ist die Teilersumme von 220 und 220 ist die Teilersumme von 284.
Das Programm errechnet Paare von befreundeten Zahlen zwischen zwei Grenzen.
Die Paare werden auf den Bildschirm und in eine Datei geschrieben.
Dank an Herrn Andreas Englisch aus München für Verbesserungen am Programm!
Das Programm herunterladen C++-Quelle
Programm "Summe von Kubikzahlen"
Ramanujan war ein indischer Mathematiker, der von 1914 bis 1919 in Cambridge wirkte. Während dieser Zeit arbeitete er mit Godfrey Harold Hardy
zusammen. Eines Tages besuchte ihn Hardy im Krankenhaus. Ramanujan, der immer an Zahlen interessiert war, fragte Hardy nach der Nummer seines Taxis.
"Ach es war die 1729. Eine völlig bedeutungslose Zahl," antwortete Hardy. Ramanujan richtete sich mühsam im Bett auf. "Keineswegs! Die Zahl 1729
ist eine sehr interessante Zahl! Es ist die kleinste Zahl, die man auf mehr als eine Art als Summe von von zwei Kubikzahlen darstellen kann."
Nach dieser Anekdote nennt man die Zahl 1729 auch die "Hardy-Ramanujan-Zahl".
1729 = 10³ + 9³ = 12³ + 1³
Das Programm berechnet Zahlen, die sich auf mehr als eine Art als Summe von zwei Kubikzahlen darstellen lassen zwischen zwei Grenzen.
Die Zahlen und ihre Darstellung als Summe von Kubikzahlen werden auf den Bildschirm und in die Datei "summekubikzahlen.txt" geschrieben.
Das Programm herunterladen C++-Quelle
Programm "Pythagoreische Zahlentripel"
Zahlentripel a, b, c, die der Gleichung a² + b² = c² genügen, nennt man Pythagoreische Zahlentripel oder Pythagoreische Tripel.
Mit folgendem Verfahren kann man teilerfremde Pythagoreische Tripel a, b, c berechnen:
Man setze
a=u² - v²
b=2uv
c=u² + v²
Weitere Bedingungen: u und v müssen teilerfremd sein, u muß größer v sein und u-v muß ungerade sein.
Die ersten solchen Paare von u und v sind:
u v (a,b,c)
2 1 (3, 4, 5)
3 2 (5, 12, 13)
4 1 (15, 8, 17)
4 3 (7, 24, 25)
Das Programm berechnet alle Pythagoreischen Tripel zwischen zwei Grenzen von u mit allen möglichen Werten von v.
Das Programm herunterladen C++-Quelle
etwas Zinsrechnung
Nehmen wir einmal an, jemand hätte aus Freude über die Geburt Christi im Jahre Null 1 Cent auf die Bank getragen. Wieviel wäre bis heute (2010) aus diesem Geld geworden?
Bei einem Zinssatz von 2%: 1,9335*1015 Euro
Bei einem Zinssatz von 4%: 1,7259*1032 Euro
Bei einem Zinssatz von 6%: 7,3247*1048 Euro
Bei einem Zinssatz von 8%: 1,5197*1065 Euro
Bei einem Zinssatz von 10%: 1,5823*1081 Euro
Nun kann man sich unter solchen Riesenzahlen nichts rechtes vorstellen. Versuchen wir es doch einmal mit Gold.
Als Basis dient uns der Goldpreis von Anfang 2010 von etwa 800 Euro pro Feinunze.
Beim Zinssatz von 2% erhalten wir eine Goldmenge von 75,2 Mio t. Das ist etwa das 500fache der gesamten Goldmenge, die jemals
auf der Erde gefördert worden ist.
Beim Zinssatz von 4% erhalten wir eine Goldmenge, deren Masse etwa das 1000fache der Erdmasse beträgt.
Die gesamte Erde würde mit einer Goldschicht bedeckt und bildet eine Goldkugel, deren Radius 43000 km beträgt.
Beim Zinssatz von 6% würde diese Goldkugel einen Radius von 1,52*1010km haben.
Das ist etwa das Hundertfache der Astronomischen Einheit (Entfernung der Erde von der Sonne) oder das Dreifache der Entfernung der Sonne zum äußersten Planeten Pluto
Beim Zinssatz von 8% erhalten wir eine Goldkugel aus massivem Gold mit einem Radius von 4,18*1015km. Das ist ein halbes Lichtjahr.
Beim Zinssatz von 10% erhalten wir eine Goldkugel mit einem Radius von 9,1*1020km. Das entspricht etwa dem Durchmesser des Milchstraßensystems.


















